Static Procedural Methods theorem (Barseghyan-2015)

This is an answer to the question Static vs. Dynamic Methods that states "All procedural methods are necessarily static."

Static Procedural Methods theorem was formulated by Hakob Barseghyan in 2015.1 It is currently accepted by Scientonomy community as the best available answer to the question.

Broader History

Philosophers of science up until Karl Popper and Imre Lakatos typically believed that there was at least one element of the scientific mosaic immune to change. For most, this static element was believed to be a transhistorical scientific method. Philosophers have not always agreed what this static method should be, but almost all until the second half of the twentieth century believed that the scientific method should be an unchanging element in a scientific mosaic.2

Aristotle and his successors assumed a method by which axiomatic proof could guarantee absolute certainty about the world. Rudolf Carnap and the logical positivists attempted to axiomatize scientific theories, and therefore apply a universal method of logical deduction in their form of inductive verificationism. Contra the positivist approach, but still assuming a universal and static characteristic of method, Popper introduced a falsificationist method of science.3 This method rejected ever achieving absolute certainty in the truth of a theory, but Popper and contemporaries nonetheless assumed that this falsificationist method ought to have, and in fact had, applied to all scientific communities across time and space. The particular differences between each method are elaborated on the page on Method, but it is due to the assumption that their own explicated procedure of theory acceptance applies to all scientific communities that these philosophers can be characterized as subscribing to a Static Methods theorem.

More recently, the debate between Laudan and Worrall4567 elucidated the distinction between two questions about static methods. First, an empirical question: have there been any methods which have not changed through history? And second, a theoretical question: Are there any methods which are, in principle, immune to change? Both Worrall and Laudan agreed that there exist substantive methods shaped by contingent proposition and therefore not static. However, Laudan held that no methods have ever been procedural — shaped by only necessary propositions and therefore immune to change — whereas Worrall contents that certain methods, such as the hypothetico-deductive method, are in fact procedural and historically have formed the base of scientific reasoning.

Scientonomic History

Acceptance Record

Here is the complete acceptance record of this theory:

Community	Accepted From	Acceptance Indicators	Still Accepted	Accepted Until	Rejection Indicators
Scientonomy	1 January 2016	The theorem became de facto accepted by the community at that time together with the whole theory of scientific change.	Yes

Question Answered

Static Procedural Methods theorem (Barseghyan-2015) is an attempt to answer the following question: Are there any methods which are immune to change?

See Static vs. Dynamic Methods for more details.

Description

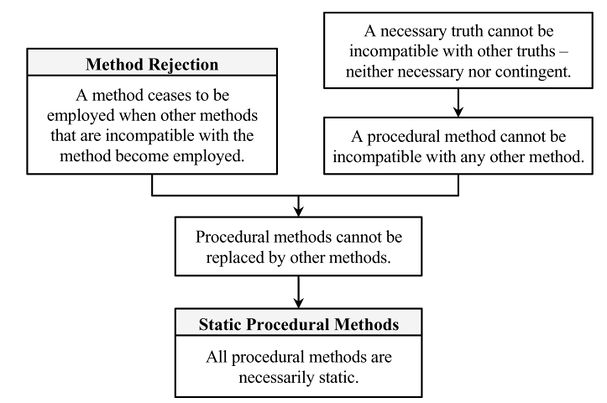
A procedural method is a method which doesn't presuppose any contingent propositions; it can only presuppose necessary truths such as those of mathematics or logic. Given the nature of necessary truths, it is impossible for one such truth to contradict another necessary truth since it must be true in all possible worlds. Therefore, it follows from the Method Rejection theorem that, since there can be no elements at odds with a necessary truth, any procedural method is, in principle, static.

Reasons

Reason: Static Procedural Methods theorem deduction

Barseghyan (2015) deduces the Static Procedural Methods theorem as follows and with the following justification:

By the method rejection theorem, a method is rejected only when other methods that are incompatible with the method in question become employed. Thus, a replacement of a procedural method by another method would be possible if the two were incompatible with each other. However, it can be shown that a procedural method can never be incompatible with any other method, procedural or substantive.

Consider first the case of a procedural method being replaced by another procedural method. By definition, procedural methods don’t presuppose anything contingent: they can only presuppose necessary truths. But two necessary truths cannot be incompatible, since necessary truths (by definition) hold in all possible worlds. Therefore, two methods based exclusively on necessary truths cannot be incompatible either; i.e. any two procedural methods are always compatible. Consequently, by the method rejection theorem, one procedural method cannot replace another procedural method. Consider a new necessarily true mathematical proposition that has been proven to follow from other necessary true mathematical propositions. By the second law, this new theorem becomes accepted into the mosaic. The acceptance of this theorem can lead to the invention and employment of a new procedural method based on this new theorem. Yet, this new method can never be incompatible with other employed procedural methods, just as the newly proven theorem can never be incompatible with those theorems which were proven earlier (of course, insofar as all of these theorems are necessary truths).

Thus, the only question that remains to be answered here is whether a procedural method can be replaced by a substantive method? Again, the answer is “no”. Substantive methods presuppose some contingent propositions about the world, while procedural methods presuppose merely necessary truths. But a necessary truth is compatible with any other truth (contingent or necessary). Therefore, no newly accepted theory can be incompatible with an accepted necessary truth. In particular, if we take the principles of pure mathematics to be necessarily true, then it follows that no empirical theory (i.e. physical, chemical, biological, psychological, sociological etc.) can be incompatible with the principles of mathematics. Consequently, a new substantive method can never be incompatible with procedural methods. Take the above-discussed abstract deductive acceptance method based on the definition of deductive inference: if a proposition is deductively inferred from other accepted propositions, it is to be accepted. It is safe to say that no substantive method can be incompatible with this requirement, for to do so would mean to be incompatible with the definition of deductive inference, which is inconceivable. Thus, a procedural method can be replaced neither by substantive nor by procedural methods.

This brings us to the conclusion that all procedural methods are in principle static.1pp. 224-225

Here is the deduction:

This reason for Static Procedural Methods theorem (Barseghyan-2015) was formulated by Hakob Barseghyan in 2015.

Edit Delete

If a reason supporting this theory is missing, please add it here.

Questions About This Theory

There are no higher-order questions concerning this theory.

If a question about this theory is missing, please add it here.