Possible Mosaic Split theorem (Barseghyan-2015)
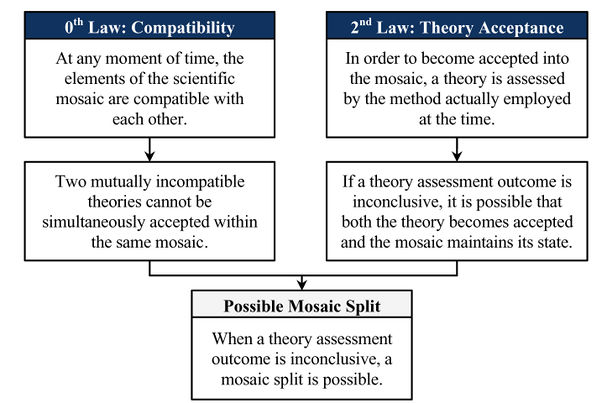
This is an answer to the question Mechanism of Mosaic Split that states "When a theory assessment outcome is inconclusive, a mosaic split is possible."
Possible Mosaic Split theorem was formulated by Hakob Barseghyan in 2015.1 It is currently accepted by Scientonomy community as the best available answer to the question.
Contents
Broader History
Like the broader topic of the Mechanism of Mosaic Split the matter of possible mosaic split has classically been regarded as a case of divergent belief systems in communities, with the caveat that the divergence in the community is contingent, not necessary. As such pre-scientonomic approaches are those that are considerate of situations in which community beliefs may diverge but will not do so necessarily.
The obvious starting point for this sort of discussion is Thomas Kuhn, for whom any case of scientific change is merely contingent owing to the nature of scientific revolutions.2pp. 146-149 In terms of the mechanism itself, Kuhn suggested that the actual process of theory choice ultimately comes down to the deliberation of values inherent to scientific endeavors, which together constitute the "shared basis for theory choice".3p. 103 A divergence within the community implies a conflict in the value-assessment that the community has undertaken when deliberating between two theories. In such cases the emergence of two distinct communities with two different sets of theories arises due to the possibility of differing beliefs with regards to values. These debates do not necessarily end in a division in the community, so it is clear that we are still within the domain of contingent divergence of belief.
Larry Laudan would later take up a model similar to Kuhn's except that Laudan more clearly explicated the role of values within a hierarchy of scientific debate.4ch. 2 Laudan's proposal was that a community could experience divergence of belief and a split in the community any time there was a disagreement at any level in the hierarchy, though this is not necessarily the case.4p. 46
Scientonomic History
Acceptance Record
| Community | Accepted From | Acceptance Indicators | Still Accepted | Accepted Until | Rejection Indicators |
|---|---|---|---|---|---|
| Scientonomy | 1 January 2016 | The theorem became de facto accepted by the community at that time together with the whole theory of scientific change. | Yes |
Question Answered
Possible Mosaic Split theorem (Barseghyan-2015) is an attempt to answer the following question: What happens to a mosaic when two or more similar theories are considered equally acceptable by a scientific community? Under what conditions does a mosaic split occur? What happens to a mosaic when it is transformed into two or more mosaics?
See Mechanism of Mosaic Split for more details.
Description
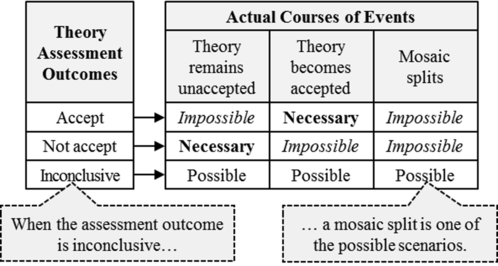
Possible mosaic split is a form of mosaic split that can happen if it is ever the case that theory assessment reaches an inconclusive result. In this case, a mosaic split can, but need not necessarily, result.1pp. 208-213 That is, "the sufficient condition for this second variety of mosaic split is an element of inconclusiveness in the assessment outcome of at least one of the contender theories".1p. 208
Barseghyan notes that, "if there have been any actual cases of inconclusive theory assessment, they can be detected only indirectly".1p. 208 Therefore:
One way of detecting an inconclusive theory assessment is through studying a particular instance of mosaic split. Unlike inconclusiveness, mosaic split is something that is readily detectable. As long as the historical record of a time period is available, it is normally possible to tell whether there was one united mosaic or whether there were several different mosaics. For instance, we are quite confident that in the 17th and 18th centuries there were many differences between the British and French mosaics.1p. 208
Thus, the historical examples of mosaic split below also serve as points of detection for historical instances of inconclusive theory assessment.
The gist of this theory can be illustrated by the following examples.
Possible Mosaic Split: Two Contender Theories
Barseghyan continues providing examples of possible mosaic split, noting that an analysis of the case in which there are two contender theories and not just one is "more illustrative".1p. 205
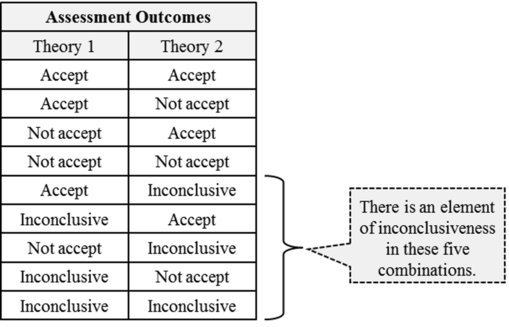
The case with two contender theories is more illustrative. When two contender theories undergo assessment by the current method, each assessment can have three possible outcomes. Therefore, there are nine possible combinations of assessment outcomes overall and, in five of these nine combinations, there is an element of inconclusiveness.1p. 205
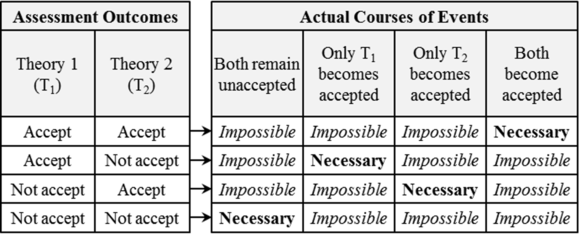
The actual course of events in the first four combinations is relatively straightforward. If the assessment of one theory yields a conclusive “accept” while the assessment of the other yields a conclusive “not accept”, then, by the second law, the former becomes accepted while the latter remains unaccepted. When the assessments of both theories yield conclusive “not accept”, then both remain unaccepted and the mosaic maintains its current state. Finally, when the assessment yields “accept” for both theories, then both theories become accepted and a mosaic split takes place, as we know from the Necessary Mosaic Split theorem (Barseghyan-2015) 1p. 205
As we can see, in each of these four cases, there is only one necessary course of events. In other words, when the assessment outcomes of both theories are conclusive, the actual course of events is strictly determined by the assessment outcomes. This is not the case with the other five combinations of assessment outcomes. Let us consider them in turn.1p. 206
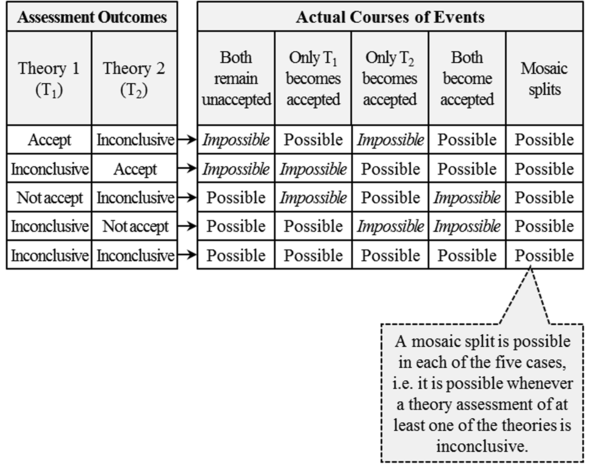
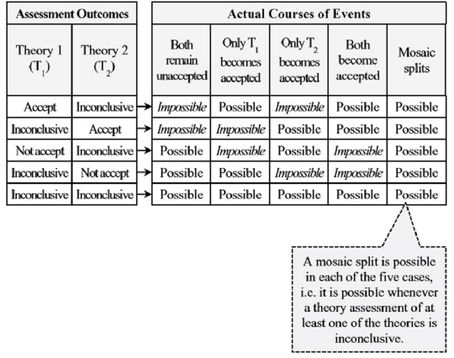
Accept/inconclusive: What can happen when the assessment of one theory yields a conclusive “accept”, while the assessment outcome of the other theory is inconclusive?
In such a scenario, the former theory must necessarily become accepted, while the latter may or may not become accepted. Therefore, only two courses of events are possible in this case: it is possible that only the former theory will become accepted and it is also possible that both theories will become simultaneously accepted (i.e. a mosaic split may take place).1p. 206
Not accept/inconclusive: What can happen when the assessment of one theory yields a conclusive “not accept”, while the assessment outcome of the other theory is inconclusive?
In such an instance, it is impossible for the former theory to become accepted, while the latter may or may not become accepted. Thus, it is possible that both theories will remain unaccepted as well as it is possible that only the latter theory will become accepted. Finally, the mosaic split is also among the possibilities, since it is conceivable that one part of the community may opt for accepting the latter theory while the other part may prefer to maintain the current state of the mosaic. Disregard for a moment the former theory: it cannot become accepted, since its assessment yields a conclusive “not accept”. With the former theory out of the picture, we are left with the latter theory – the one with an inconclusive assessment outcome. Thus, this case becomes similar to the above-discussed case with only one contender theory: we have a contender with an inconclusive assessment outcome and, consequently, a mosaic split may take place provided that one part of the community decides to opt for the theory while the other part prefers to stick to the existing mosaic. Note that, in this case, a split is not a consequence of the simultaneous acceptance of two mutually incompatible theories.1pp. 206-207
Inconclusive/inconclusive: Finally, what can happen when the assessment outcomes of both theories are inconclusive?
In such a scenario, both theories may or may not become accepted. Thus, it is possible that none of the theories will become accepted, just as it is possible that only one of the two will become accepted. It is also possible that both theories will become simultaneously accepted and, consequently, a mosaic split will take place.1p. 207
Therefore, Barseghyan concludes through this meticulous example that "a mosaic split is possible in those cases where the assessment outcome of at least one contender theory is inconclusive".1p. 207
Possible Mosaic Split: Drug Trials
Suppose we have a method for assessing theories about the efficacy of new pharmaceuticals that says "accept that the pharmaceutical is effective only if a clinically significant result is obtained in a sufficient number of randomized controlled trials." The wording of the method is such that it requires a significant degree of judgement on the part of the community - what constitutes 'clinical significance' and a 'sufficient number' of trials will vary from person to person and by context. This introduces the possibility of mosaic split when it is unclear if two contender theories satisfy this requirement.
Carrying on the above example, suppose two drugs are being tested for some condition C: drugs A and B. We'll call T1 the theory that A is more effective than B at treating condition C and T2 the theory that B is more effective than A at treating condition C. These two theories are not compatible, and so cannot both be elements of the mosaic according to the zeroth law. Suppose further that both are assessed by the method of the time, meaning that both are subject to double blind trials. In these trials drug A is clearly superior to drug B at inducing clinical remission, but drug B has fewer side effects and is still more effective than a placebo and has had more studies conducted. Even if we accept T1 we may have reason to suspect that T2 better satisfies the method. We can interpret this in two ways: by supposing that our assessment shows that we should accept T1 and that our assessment is inconclusive about T2 or by taking both assessments to be inconclusive. In the first case it is permissible according to the second law to accept T1 and to either accept or reject T2, and in the second case both may be accepted or rejected.
Because any time an assessment outcome is inconclusive we may either accept or reject the theory being assessed we always face the possibility that one subsection of the community will reject the theory and another subsection will accept it. In these cases the two communities now bear distinct mosaics and a mosaic split has occurred. However it is important to note that the ambiguity inherent in inconclusive assessments means that it is never entailed that there will be competing subsections of the community. A community may, in the face of an inconclusive assessment, collectively agree to accept or reject the theory being assessed. Thus, in cases with an inconclusive assessment mosaic split is possible but never necessarily entailed by the circumstances.Possible Mosaic Split: One Contender Theory
Barseghyan's example of mosaic split which may result from one contender theory, proceeds as follows.
Consider first the case with one contender theory. Suppose there is a scientific mosaic with its theories and methods and there is also a contender theory which becomes assessed by the currently employed method. If the assessment outcome is conclusive “accept”, the theory necessarily becomes accepted. If the outcome is conclusive “not accept”, the theory remains unaccepted. Both of these cases are quite straightforward. But what will happen if the outcome turns out to be inconclusive, i.e. if the assessment by the current method doesn’t provide a definitive prescription? When the assessment outcome is inconclusive, there are three possible courses of events. First, the new theory can remain unaccepted; in that case the mosaic will maintain its current state. Second, the new theory can also become accepted by the whole community; in that case a regular theory change will take place and the new theory will replace the old one. None of these two scenarios is particularly interesting here. However, there is also the third possible course of events. When the outcome of theory assessment is inconclusive, members of the community are free to choose whichever of the two scenarios – they can accept the theory, but they can equally choose to leave it unaccepted. Naturally, there are no guarantees that all of them will necessarily choose the same course of action. It is quite conceivable that some will opt for accepting the new theory, whereas the rest will prefer to keep the old theory. In other words, when the assessment of a contender theory yields an inconclusive outcome, the mosaic may split in two.1pp. 204-205
Possible Mosaic Split: Acceptance of the Cartesian natural philosophy in Cambridge circa 1680.
Barseghyan (2015) contrasts the replacement of the Aristotelian-Medieval method with the Newtonian method in Britain and the Cartesian method in France -- a broad case which might seem like an instance of mosaic split, but is not -- with a more specific historical example of potential mosaic split. He outlines that specific historical example, the acceptance of the Cartesian natural philosophy in Cambridge circa 1680, as follows:
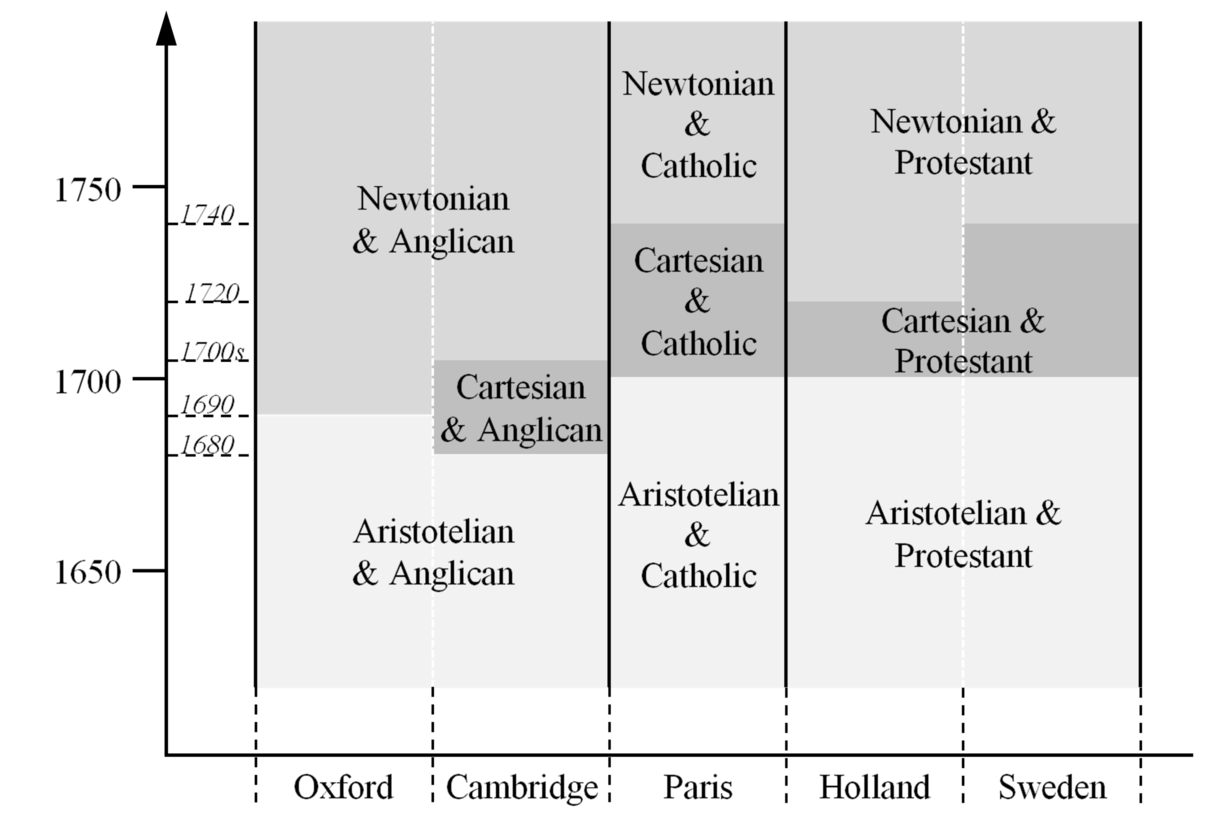
Let us begin with the available historical data. Prior to the 1680s, the Aristotelian-medieval natural philosophy was taught in schools across Europe, with alternative theories included into the curricula only sporadically. If my understanding is correct, the first university where the Cartesian natural philosophy was accepted and taught on a regular basis was Cambridge. Although the theory had been sporadically taught since the 1660s, it began to be taught systematically only circa 1680.379 Thus, it is not surprising that when one Cambridge professor Isaac Newton was writing his magnum opus, the main target of his criticism was Descartes’s theory, not that of Aristotle. According to the historical data, during the last two decades of the 17th century, Cambridge remained the only university where the Cartesian theory was generally accepted. The situation changed circa 1700, when the Cartesian natural philosophy together with its respective modifications by Huygens, Malebranche and others became accepted in France, Holland and Sweden. As for Oxford, it never accepted the Cartesian theory but switched directly to the Newtonian theory circa 1690. In Cambridge, the transition from the Cartesian natural philosophy to that of Newton took place in the 1700s. Most likely, the universities of the Dutch Republic (Leiden and Utrecht) were the first on the Continent to accept the Newtonian theory by 1720. In France and Sweden, the Newtonian theory replaced the Cartesian natural philosophy circa 1740.386 The picture wouldn’t be complete if we didn’t mention the important theological differences: Catholic theology was accepted in Paris; Anglican theology was accepted in Oxford and Cambridge; in Holland and Sweden the accepted theology was that of Protestantism.1pp. 211-212
A draft timeline of the situation, including theological differences, at the end of the 17th century has been constructed by Barseghyan:
Barseghyan (2015) continues as follows:
Although the diagram hardly scratches the surface of the colorful 17-18th century landscape, it points to at least two possible candidates of mosaic split. Apparently, there seem to have been a split in the Anglican mosaic of Britain circa 1680, when the Cartesian natural philosophy became accepted in Cambridge, and also probably in the Protestant mosaic sometime by 1720, when the Newtonian theory became accepted in Holland.1pp. 212
Barseghyan (2015) more closely examines the first potential case: the acceptance of Cartesian natural philosophy in Cambridge:
If my reading is correct, then this was a typical case of mosaic split: after the acceptance of the Cartesian theory, the mosaic of Cambridge became different from the Aristotelian-Anglican mosaic of other British universities. Note that this mosaic split was caused by the acceptance of only one new theory. Therefore, it could only be a result of an inconclusive theory assessment. At this point, we can only hypothesize as to why exactly the outcome of the assessment of the Cartesian theory was inconclusive. My historical hypothesis is that it had to do with the inconclusiveness of the Aristotelian-medieval method employed at the time, i.e. with the vagueness of the implicit expectations of the community of the time.
It is easily seen that the then-employed Aristotelian-medieval method allowed for two distinct scenarios of theory assessment. On the one hand, if a proposition was meant as a theorem, it was only expected to show that it did in fact follow from other accepted propositions. That much would be sufficient for a new theorem to become accepted. This part of the method is straightforward – no ambiguity here. If, on the other hand, a proposition was not meant as a theorem – if it was supposed to be a separate axiom – then it was expected to be intuitively true. But what does it mean to be intuitively true? Nowadays we seem to realize that no proposition can be intuitively true (unless of course it is a tautology) and that intuition, even when “schooled by experience”, is not the best advisor in theory assessment.66 Therefore, a theory could merely appear intuitively true to the community of the time. This was the actual expectation of the scientific community in the 17th century – the appearance of intuitive truth. One indication of this is the fact that both Descartes and Newton understood the vital necessity of presenting their systems in the axiomatic-deductive form. They also made all possible efforts to show that their axioms – the starting points of their deductions – were beyond any reasonable doubt. They both realized that if their theories are ever to be accepted, their axioms must appear clear to anyone who is knowledgeable enough to understand them. But this is exactly what was expected by the scientific community of the time. Yet, the requirement of intuitive truth is extremely vague: what appears intuitively true to me need not necessarily appear intuitively true to others.
I think this can explain why the mosaic split of the 1680s took place. The axioms of the Cartesian natural philosophy were meant as self-evident intuitively true propositions. But as with any “intuitive truth”, scientists could easily disagree as to whether the axioms were indeed intuitively true. As a result, the outcome of the assessment of the Cartesian theory was “inconclusive”. In that situation, a mosaic split was one of the possible courses of events (by the possible mosaic split theorem). Of course the mosaic split wasn’t inevitable – it was merely one of the possibilities which actualized. This Aristotelian “bring before me intuitive true propositions” requirement was so vague that theory assessment could easily yield an “inconclusive” outcome and, consequently, result in a mosaic split. It is not surprising, therefore, that the British mosaic did actually split in the 1680s when the Cartesian natural philosophy was accepted only in Cambridge. This was an instance of possible mosaic split.1pp. 212-213
Reasons
Reason: Deduction of the Possible Mosaic Split theorem
The possible mosaic split theorem follows as a deductive consequence of the second and zeroth laws, given a situation a situation where the assessment of two theories obtains an inconclusive result. This will happen when it is unclear whether or not a theory satisfies the employed method of the community.
This reason for Possible Mosaic Split theorem (Barseghyan-2015) was formulated by Hakob Barseghyan in 2015.1
If a reason supporting this theory is missing, please add it here.
Questions About This Theory
There are no higher-order questions concerning this theory.
If a question about this theory is missing, please add it here.
References
- a b c d e f g h i j k l m n o p q r Barseghyan, Hakob. (2015) The Laws of Scientific Change. Springer.
- ^ Kuhn, Thomas. (1962) The Structure of Scientific Revolutions. University of Chicago Press.
- ^ Kuhn, Thomas. (1977) The Essential Tension: Selected Studies in Scientific Tradition and Change. University of Chicago Press.
- a b Laudan, Larry. (1984) Science and Values. University of California Press.